Punk rock
Published: Monday 11 November 2024 at 22:43
I was searching for some new music yesterday, and stumbled on the latest album of Melbourne punk band Amyl and the Sniffers. I listened to a few of their songs and liked their sound and lyrics - they've got that thing going where it feels like it's all very real and not the result of many iterations of refinement. A mood I associate strongly with what punk is all about to me - a rejection of authority.
Thoughts on inflation targets.
Published: Tuesday 15 October 2024 at 22:02
An nescis, mi fili, quantilla prudentia mundus regatur?
When reading Friedrich August von Hayek's Nobel Prize lecture given in 1974, my mind drifted immediately to the idea that central banks all over the world have taken for truth: we should have inflation in a band of two to three percent to achieve good economic outcomes for a country, and we have one tool to achieve that outcome - a target interest rate determined by committee.
On writing notes
Published: Saturday 30 March 2024 at 16:40
Over the month of March, my interest veered to the area of personal knowledge management. This was triggered reading a blog post by Mark Bernstein. He is the author of a software tool called Tinderbox. The post linked to a series of videos where users of the tool explain how it helps them in their endeavours. The one by Stacey Mason on goal setting was inspiring - so cool to see how someone is able to set goals for both her professional and her personal life and use those to improve her relationships, her career and general wellbeing. Maybe the most convincing about the whole concept is seeing it in action on this forum. Not only is the video of the event available, but key quotes are also extracted and resources like books, videos or websites to review are there to immediately go deeper or further into a subject.
Sydney's Red Rooster line.
Published: Tuesday 27 February 2024 at 22:27
Listening to ABC Radio National a couple of weeks ago, I learned about Sydney's Red Rooster line. It's a straight line that can be drawn across Sydney marking the socio-economic divide that exists between the northern and eastern suburbs of Sydney and the western and soutwestern ones. Out of curiosity, I set out to explore this using data available on the open web, in particular OpenStreetMap.
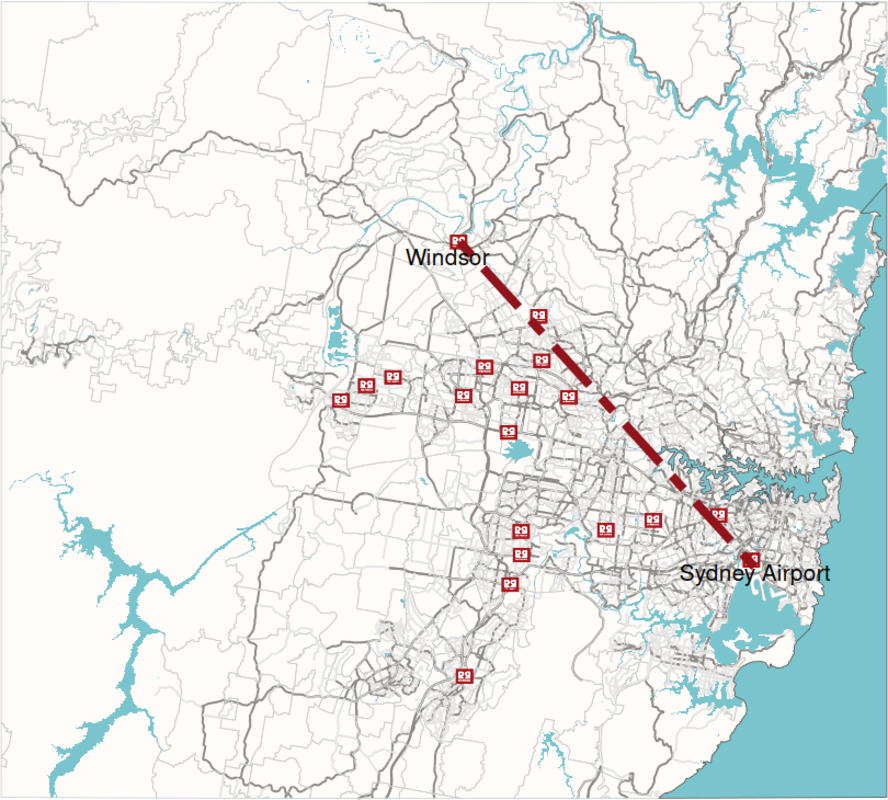
The above map was drawn in R using OpenStreetMap data for all its components.
My year in books.
Published: Monday 15 January 2024 at 21:27
I compiled an overview of the books I finished in 2023, including the language I read them in. During this year, I did most of my book reading on an e-reader (Kobo Clara 2nd edition), and the list only reflects these. I'm pleased with having read a book in French, which I also finished while on holidays, adding to the positive memories of it. Using an e-reader was very helpful there - I could look up words I didn't know without having to step out of the book thanks to the in-built dictionaries.
Early on in the year, I decided I'd try to read some classics from Dutch language writers, and that didn't disappoint. Harry Mulish's De ontdekking van de wereld, finished on the last day of 2023, was the best read of the year, although The lord of the rings would possibly have taken that spot had I not read it before.
Volunteering at Seeds for Snapper
Published: Tuesday 2 January 2024 at 18:38
During the 2023 end-of-year holiday season, I joined a group of colleagues at OzFish Seeds for Snapper to help out collecting seagrass seeds from the beach at Woodman Point. We were told about the importance of seagrass to help protect young fish and in particular pink snapper in the Cockburn Sounds. Our assistance was mostly informative this year, as the fruiting of the seagrass had happened over a much shorter time window than in previous years, and had yielded relatively few seeds. Connecting with Synergy colleagues I don't usually interact with was great in itself though, as was learning about the different kinds of seagrass found in Australian waters. I was most impressed finding out the seagrass 'up North' around Shark Bay largely stems from the same plant, which reproduces asexually. Spanning more than 180km, it is the most widespread known clone on earth.
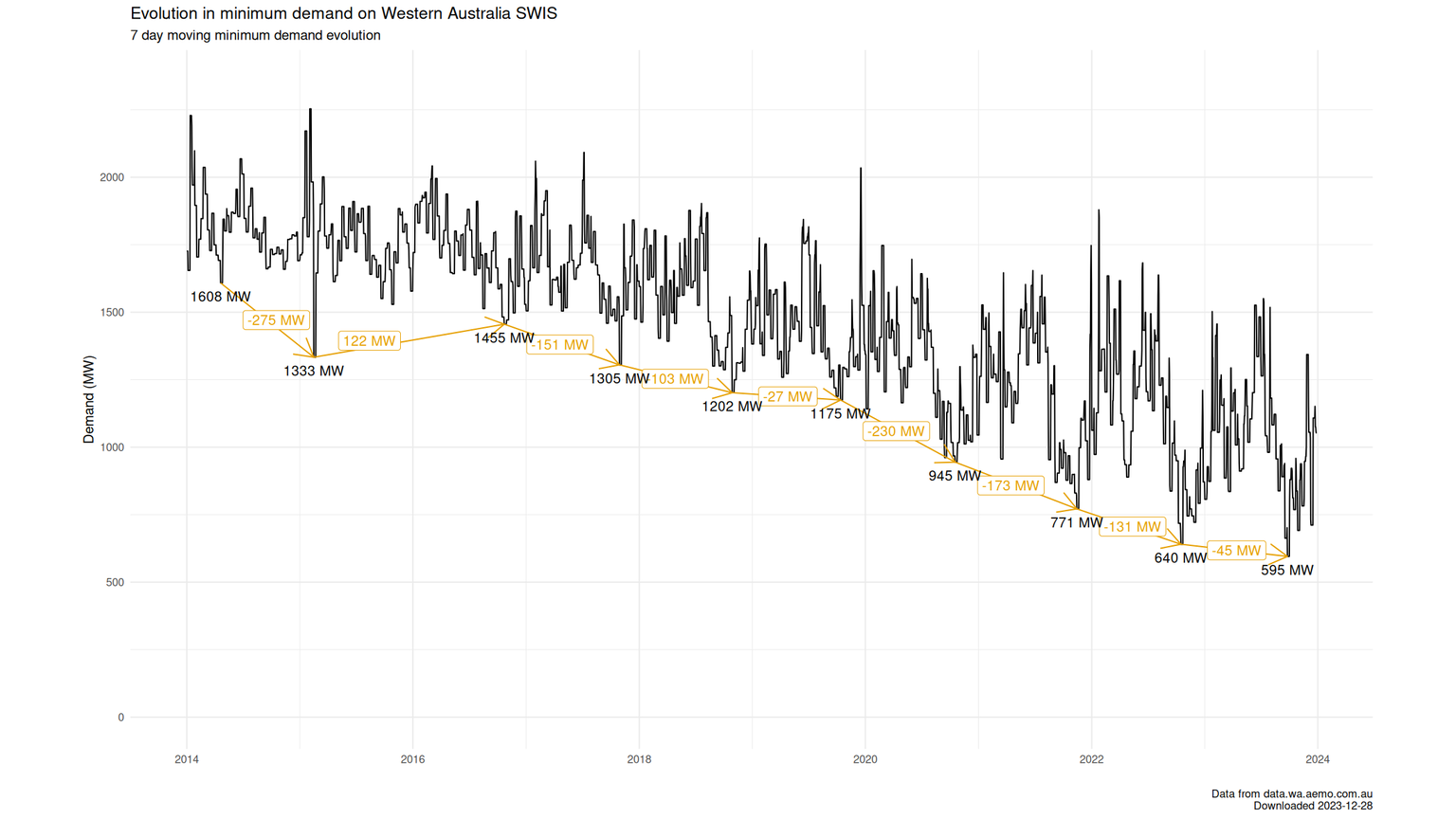
How the energy transition is replacing daytime electricity generation.
Published: Thursday 28 December 2023 at 21:52
In a process labelled the energy transition, traditional sources for electricity generation are being replaced by renewable energy sources like wind and solar. To the extent this happens 'behind the meter', i.e. where the user of the electricity is generating & consuming it on their own premises like with rooftop solar panels, it results in the metered demand on the electricity grid not being aware of the demand that is met by on-site generation. Given how prevalent solar panels have become on Western Australian roofs over the past 10 years, it might not come as a surprise this has resulted in the remaining demand on the grid to come down on very sunny days around noon. This reduction has been quite rapid for a couple of years, but seems to have slowed this year and last, as seen in the graph below.
About sending pingbacks, webmentions and some thoughts on how to improve on them.
Published: Tuesday 31 October 2023 at 20:41
In a 'blast from the past', I sent my first pingback after writing the previous post. A pingback is a way for a blogger to send a message to another blogger, informing them they've written a post that refers to theirs, e.g. as a reply or an extension of the ideas raised.
The process is a bit more involved than using a webmention, which I've used before and implemented support for a while back, due to requiring an XML message to be created rather than a simple exchange of URLs.
Agent-based models and digital twins.
Published: Sunday 29 October 2023 at 07:15
A new approach to modeling using categories and software, facilitating the build of advanced models like digital twins, is being developed at the moment.
Obtaining WA Landgate Shared Location Information using R.
Published: Wednesday 11 October 2023 at 23:41
Six years ago, I wrote about Simple Features (sf) in R. I mapped the number of pupils per high school in the Perth metro area. At the time, I didn't include how to obtain the shapefile, provided as open data by Landgate on behalf of the Western Australian government through its Shared Location Information Platform (SLIP).
House price evolution.
Published: Saturday 2 September 2023 at 16:01
Back in May 2022, I made a bet Australian house prices would decline relative to Belgian ones, and the Australian cash rate wouldn't grow as high as the Euro-zone one. On that day, the RBA had lifted the Australian cash rate from the historical low of 0.10% to 0.35%. Today, that rate stands at 4.10%, with the latest increase in a series of 12 having happened at the start of June 2023 - an increase of 4%pt.
Half Time Oranges
Published: Friday 25 August 2023 at 21:36
Moving countries means learning about a new culture. Even after 10 years in Australia, I am still discovering quirky things people raised here don't think twice about. One of these is the tradition of cutting up oranges for kids playing sports to eat during their half-time. It's not just any fruit - it simply always is oranges. It doesn't have to be oranges, except that it does, as this is just what people expect. Such a lovely tradition! Tomorrow is already the last competition day of netball in WA for the 2023 season, and my first as the parent responsible to bring in the oranges.
Perth solar exposure over year
Published: Sunday 11 June 2023 at 13:27
Perth, Western Australia is a sunny place, as any local will confirm. Combined with subsidised buyback tariffs for electricity returned into the grid, this has resulted in many local households now having an array of solar panels on their roof.
I bought a balance board.
Published: Saturday 27 May 2023 at 16:44
With summer having come to an end over here in Western Australia, the wind-filled afternoons are also behind us for a few months. While the prevailing easterlies that now reign make for glassy ocean conditions, they're generally not strong enough for wing surfing. Most Autumn days don't bring enough swell to go out surfing either around the area I live. This prompted me to try out a new activity - balance boarding.
Implementing Webmention on my blog
Published: Sunday 14 May 2023 at 20:32
Following on from my last post on joining the indieweb… Back in February, I implemented Webmentions on my website. I took a roll-my-own approach, borrowing from an idea by superkuh. It's a semi-automated solution which listens for webmentions using nginx. When (if) one is received, an email is generated that tells me about this, allowing me to validate it's a genuine comment.
Innovate WA 2023
Published: Wednesday 15 February 2023 at 17:04
Public Sector Network's Innovate WA conference today started with a poll amongst the attendees, asking for our biggest goal or aspiration for the public sector in Western Australia. Overwhelmingly, collaboration came out as the main opportunity for contributors and decision makers in the sector. Closely linked was the desire to better share data between government departments and functions. In his opening address, WA Minister for Innovation Stephen Dawson touched on that, mentioning the State Government is planning to introduce legislation later this year around privacy and responsible data sharing. This will be the first time WA government agencies and state-owned enterprises will be subject to privacy laws, and at the same time is hoped to encourage data sharing that should result in better outcomes for citizens of the state.
Bring Back Blogging
Published: Monday 2 January 2023 at 19:35
After setting a personal objective late last year of reaching 'level 2' on the indieweb, with the ability to send Webmentions, I stumbled on Bring Back Blogging yesterday. I love how some people are dedicated to keeping a decentralised internet available and of relevance.
Ronald McDonald House
Published: Thursday 22 December 2022 at 06:28
Synergy's Pricing and Portfolio team took the opportunity at the end of the year to volunteer for Ronald McDonald House Nedlands. This is a charity providing a 'home away from home' for families with a child in hospital in Perth. These families often live hundreds if not thousands of kilometers away due to the size of Western Australia, with Perth the only metropolitan area in the state featuring a children's hospital. Families often stay for weeks and even months in the facility while their child undergoes treatment.
WADSIH talk on consumer insights
Published: Sunday 6 November 2022 at 23:14
I recently had the honour of giving a talk about delivering consumer insights at a publicly owned utility during a session organised by the Western Australian Data Science Innovation Hub (WADSIH). During the talk, I walked through the data science process the team moves through while delivering customer insights. To make that less theoretical, I did this using an example of work delivered recently to prompt consumers to take mutually beneficial actions to both lower their power bills and help ensure the stability of the electricity grid.
Monetary policy and mortgage products.
Published: Monday 9 May 2022 at 18:48
In its latest statement on monetary policy (Internet Archive), the Reserve Bank of Australia highlighted that households in Australia have much higher private debt than before. Total private debt is approximately 120% of GDP (Internet Archive), roughly double Belgium's. Analysts hint this will restrict by how much the central bank will be able to raise the cash rate target (Internet Archive) to battle rising inflation in the near future.
Creating a golden spiral in R
Published: Monday 16 September 2019 at 22:03
After having read the first part of a Rcpp tutorial which compared native R vs C++ implementations of a Fibonacci sequence generator, I resorted to drawing the so-called Golden Spiral using R.
Different spin to competing on analytics.
Published: Tuesday 11 June 2019 at 20:46
The May/June 2019 issue of Foreign Affairs contains an article by Christian Brose, titled "The New Revolution in Military Affairs".
Setting up an analytics practice.
Published: Tuesday 9 April 2019 at 07:59
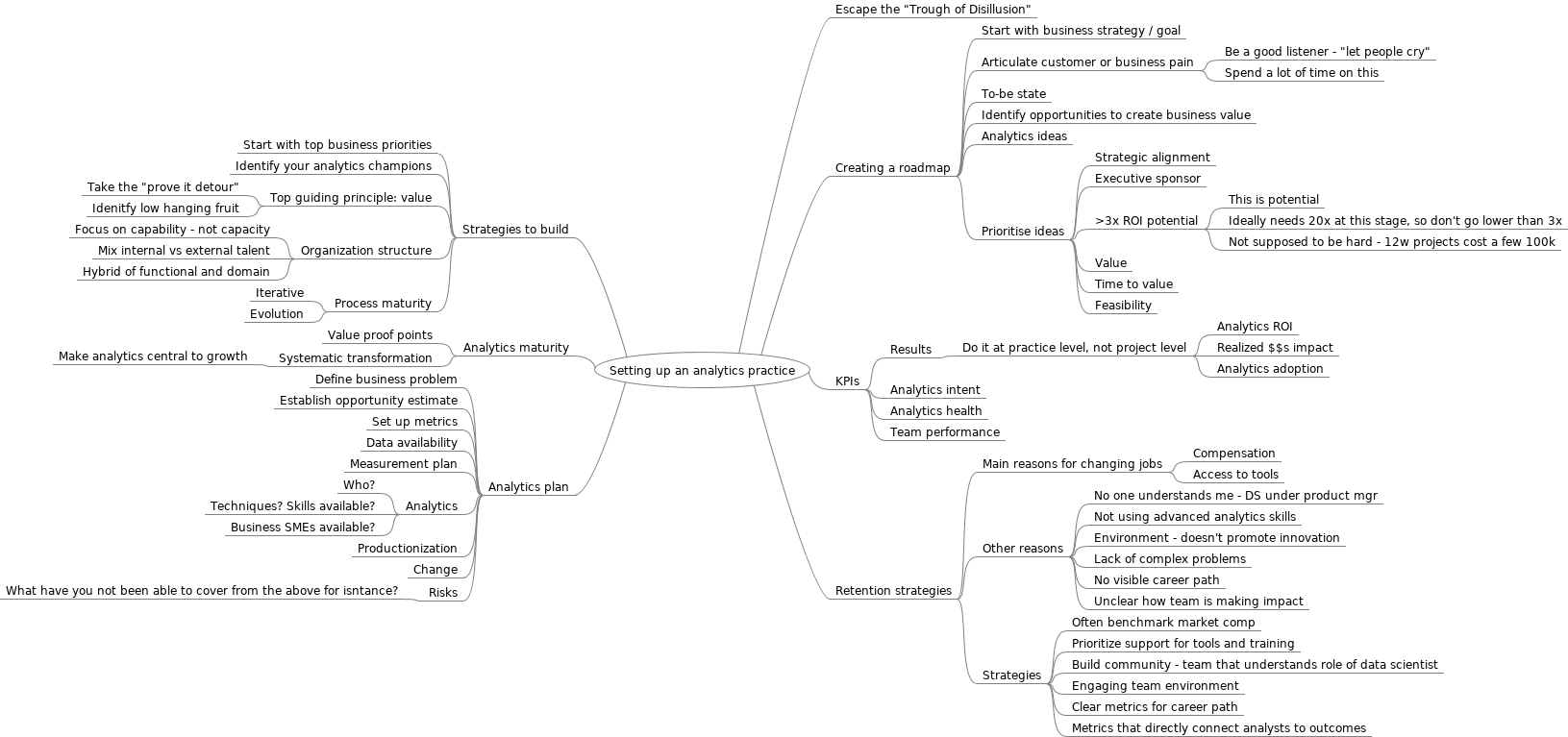
Figure 1: Mindmap on setting up analytics practice
Nobel prize winner having fun; using Jupyter notebooks.
Published: Friday 12 October 2018 at 20:00
Paul Romer may well be the first Nobel prize winner using Jupyter notebooks in his scientific workflow. On his blog, he explains his reasoning.
Wrapping Confluent Kafka in REST API using R.
Published: Friday 14 September 2018 at 21:53
It started of as an attempt to analyse some data stored in Apache Kafka using R, and ended up becoming the start of an R package to interact with Confluent's REST Proxy API.
Using Apache Nifi and Kafka - big data tools
Published: Tuesday 11 September 2018 at 21:09
Working in analytics these days, the concept of big data has been firmly established. Smart engineers have been developing cool technology to work with it for a while now. The Apache Software Foundation has emerged as a hub for many of these - Ambari, Hadoop, Hive, Kafka, Nifi, Pig, Zookeeper - the list goes on.
Managing data science work
Published: Tuesday 19 June 2018 at 20:51
It appears to me the cross-industry standard process for data mining (CRISP-DM) is still, almost a quarter century after first having been formulated, a valuable framework to guide management of a data science team. Start with building business understanding, followed by understanding the data, preparing it, moving from modeling to solve the problem over to evaluating the model and ending by deploying it. The framework is iterative, and allows for back-and-forth between these steps based on what's learned in the later steps.
My management style - mission control.
Published: Wednesday 14 February 2018 at 15:38
I have been asked a few times recently about my management style. First, while applying for a position myself. Next, less expected, by a member of the org I joined as well as by a candidate I interviewed for a position in the team.
On social media
Published: Monday 8 January 2018 at 21:04
Dries Buytaert wrote last week about intending to use social media less in 2018. As an entrepreneur developing a CMS, he has a vested interest in preventing the world moving to see the internet as being either Facebook, Instagram or Twitter (or reversing that current-state maybe). Still, I believe he is genuinely concerned about the effect of using social media on our thinking. This partly because I share the observation. Despite having been an early adopter, I disabled my Facebook account a year or two ago already. I'm currently in doubt whether I should not do the same with Twitter. I notice it actually is not as good a source of news as classic news sites - headlines simply get repeated numerous times when major events happen, and other news is equally easily noticed browsing a traditional website. Fringe and mainstream thinkers alike in the space of management, R stats, computing hardware etc are a different matter. While, as Dries notices, their micro-messages are typically not well worked out, they do make me aware of what they have blogged about - for those that actually still blog. So is it a matter of trying to increase my Nexcloud newsreader use, maybe during dedicated reading time, and no longer opening the Twitter homepage on my phone at random times throughout the day, and conceding short statements without a more worked out bit of content behind it are not all that useful?
NYC taxi calendar fun
Published: Thursday 30 November 2017 at 21:36
The Internet Archive contains a dataset from the NYC Taxi and Limousine Commission, obtained under a FOIA request. It includes a listing of each taxi ride in 2013, its number of passengers, distance covered, start and stop locations and more.
Spatial indexes to plot income per postal code in Australian cities.
Published: Thursday 16 November 2017 at 15:07
Trying to plot the income per capita in Australia on a map, I came across a perfectly good reason to make good use of a spatial query in R.
Fertile summers.
Published: Thursday 26 October 2017 at 13:06
In the Northern hemisphere, it's commonly said women prefer to give birth around summer. It would appear this does not hold for Australia. The graph below actually suggests most babies are conceived over the summer months (December to February) down under!
WA roads in R using Spatial Features.
Published: Tuesday 17 October 2017 at 20:35
How cool is this? A map of Western Australia with all state roads marked in only 5 lines of R!
Using spatial features and openstreetmap
Published: Thursday 12 October 2017 at 21:30
Turns out it is possible, thanks to the good folks at Stamen Design, to get fairly unobtrusive maps based on the OpenStreetMap data.
Explore Australian road fatalities.
Published: Tuesday 10 October 2017 at 16:56
Recently inspired to doing a little analysis again, I landed on a dataset from https://bitre.gov.au/statistics/safety/fatal_road_crash_database.aspx, which I downloaded on 5 Oct 2017. Having open datasets for data is a great example of how governments are moving with the times!
Loans and semi-Markov chains
Published: Friday 17 February 2017 at 20:07
Using Markov chains' transition matrices to model the movement of loans from being opened (in a state of "Current") to getting closed can misinform the user at times.
AUC and the economics of predictive modelling.
Published: Wednesday 11 January 2017 at 04:12
The strenght of a predictive, machine-learning model is often evaluated by quoting the area under the curve or AUC (or similarly the Gini coefficient). This AUC represents the area under the ROC line, which shows the trade-off between false positives and true positives for different cutoff values. Cutoff values enable the use of a regression model for classification purposes, by marking the value below and above which either of the classifier values is predicted. Models with a higher AUC (or a higher Gini coefficient) are considered better.
Survival analysis in fintech
Published: Saturday 10 December 2016 at 15:49
It is useful to apply the concepts from survival data analysis in a fintech environment. After all, there will usually be a substantial amount of time-to-event data to choose from. This can be website visitors leaving the site, loans being repaid early, clients becoming delinquent - the options are abound.
Using R to automate reports
Published: Monday 10 October 2016 at 21:48
A lot of information on knitr is centered around using it for reproducible research. I've found it to be a nice way to make abstraction of mundane reporting though. It is as easy as performing the necessary data extraction and manipulation in an R script, including the creation of tables and graphs.
Facet labels in R.
Published: Wednesday 5 October 2016 at 21:48
Getting used to the grammar of ggplot2 takes some time, but so far it's not been disappointing. Wanting to split a
scatterplot by segment, I used facet_grid. That by default shows a
label on each subplot, using the values in the variable by which the
plot is faceted.
Generating album art on N9.
Published: Monday 3 October 2016 at 21:33
For unknown reasons, the Music application on my Nokia N9 does not always display the album cover where expected. Instead, it displays the artist name and album title. Reports by other users of this phone suggest this isn't an uncommon issue, but offer no confirmed insight in the root cause of the problem unfortunately.
R and Github
Published: Friday 23 September 2016 at 19:47
Where my first R package was more a
proof-of-concept, I now certainly left the beginneRs group by
publishing an R package to a private Github repository at work. I used
that package in some R scripts performing various real-time analysis of
our operations already. This by loading it through the
devtools package, and specifically the install_github() function.
Fun with RJDBC and RODBC.
Published: Friday 24 June 2016 at 14:17
I have learned the hard way it is important to be aware that
Obnam for multi-client encrypted backups.
Published: Thursday 9 June 2016 at 20:41
Trying to configure obnam to use one repository for 3 clients using encryption has been a bit of search.
First R package.
Published: Wednesday 18 May 2016 at 21:09
Continuing a long tradition with announcing firsts, I wrote an R package recently, and made it available on Projects, a new section of the website. (Talking about my website on said website is also not exactly new.)
Azure file storage blobs
Published: Friday 6 May 2016 at 20:10
Azure's files storage blobs are currently not mountable from GNU/Linux, except if the box is running in the same Azure region as the blob. Theoretical solution: mount it on a VM, and sshfs that from anywhere. TBC.
New blog activated
Published: Thursday 5 May 2016 at 21:54
Going back to the early days of this site, I added a blog section in again, replacing the social one, which was overkill. Still need to import the posts done there though.
In the pines
Published: Monday 9 November 2015 at 02:20
Unplugged in New York.
Sidetracked - The Triffids.
Back to start in one hop. #inthepines
State of SaaS
Published: Sunday 8 November 2015 at 01:09
Nov 2015. Still no Mailpile 1.0. Roundcube Next MIA. Lest we forget, no Freedom Box.
Fearless analysis
Published: Saturday 22 August 2015 at 01:47
'There is no silver bullet': Isis, al-Qaida and the myths of terrorism
Magna Carta
Published: Monday 15 June 2015 at 12:59
The spirit of Magna Carta could serve us well today.
FedEx marries TNT.
Published: Tuesday 7 April 2015 at 20:05
Well, that one has been in the works for a while! Buying a solid European network for two-thirds of what UPS was willing to pay for it a few years ago sounds like a great deal.
Bluetooth
Published: Friday 27 March 2015 at 01:24
Wondering which bluetooth chipsets have free firmware. Debian non-free contains Broadcom firmware, but are more ndiswrapper tricks needed for others?
Debian on A20
Published: Tuesday 17 March 2015 at 04:08